Asymptotic Analysis
漸近分析 - 演算法時間與空間複雜度分析
什麼是好的程式碼
- Readable
- Scalable 的衡量分為:
- 空間複雜度(Space Complexity)︰執行演算法花費的記憶體空間。
- 時間複雜度(Time Complexity)︰執行演算法時須花費的時間。
Big O 用來衡量不同演算法時間複雜度, 當處理的資料量持續增加時,程式執行時間增加的比率
Asymptotic Notation
- 漸近符號
- 分析結果粗略分類可得最差情況、最佳情況、平均情況等,幾種漸進式表達方法如下
- Big-O ( Ο ):演算法時間函式的上限(Upper bound)即最糟情況下的執行次數
- describes the set of all algorithms that run no_worse than a certain speed (it’s an upper bound)
- It’s a complexity that is going to be less or equal to the worst case
- Omega ( Ω ):演算法時間函式的下限(Lower bound)
- describes the set of all algorithms that run no_better than a certain speed (it’s a lower bound)
- It’s a complexity that is going to be at least more than the best case
- Theta ( θ ):演算法時間函式的上限與下限之間
- describes the set of all algorithms that run at a certain speed (it’s like equality)
- It’s a complexity that is within bounds of the worst and the best cases
- Big-O ( Ο ):演算法時間函式的上限(Upper bound)即最糟情況下的執行次數
Time of Complexity
- 時間複雜度
| Complexity | Name | Desc. |
|---|---|---|
O(1) | Constant | Accessing a specific element in array |
O(N) | Linear | Loop through array elements |
O(log N) | Logarithmic | Find through array elements |
O(N²) | Quadratic | Looking at every index in the array twice |
O(2^N) | Exponential | Double recursion in fibonacci |
Equation - Asymptotic Complexity
當 n = 1 時:
5n²→5/23 = 21.74%6n→6/23 = 26.09%12→12/23 = 52.17%
看起來常數 12 佔比最大,但當我們觀察增長率:
| n | 5n² | 6n | 12 |
|---|---|---|---|
| 10 | 87.41% | 10.49% | 2.09% |
| 100 | 98.79% | 1.19% | 0.02% |
| 1000 | 99.88% | 0.12% | 0.0002% |
設 f(n) = n,g(n) = 2n,問 f(n) = O(g(n)) 是否成立?
取 c = 1,n = 1:n ≤ 1·2n ✓
設 f(n) = 4n + 3,g(n) = n
取 c = 5:4n + 3 ≤ 5n ✓
O(1)
- Constant time
- Random access of an element in an array
- Inserting at the beginning of linkedlist
- 陣列讀取
- 沒有迴圈,執行時間不會隨輸入的資料量增加而增加。
int[] array = {1, 2, 3, 4, 5}
array[0] // It takes constant time to access first elementO(log n)
- Logarithmic time
- since it is visiting only some elements
- Binary Search
- Searching Algorithms that finds the position of a target value within a sorted array. Half of the array is eliminated during each “Step”.
- Working on Large Data Sets like millions data is good
- 二分搜尋 : 資料經過排序(sorted),資料可以對半處理
O(n)
- Linear Search : Iterate through a collection one element at a time
- Looping through elements in an array : 簡易搜尋
- Searching through a linkedlist
- Cons :
- Slow for large data sets
- Pros :
- Fast for searches of searches to small to medium data sets
- Does not need to sorted
- Useful for data structures thart do not have random access (Linked List)
- e.g.
int[] array = {1, 2, 3, 4, 5}
for(int i = 0; i < array.length; i++){
System.out.println(array[i]);
}O(n log n)
- Quasilinear Time
- Quick Sort
- Merge Sort : 合併排序
- Heap Sort
- 通常處理排序 (Sorting) 的操作
O(n²)
- Quadratic time
- Insertion Sort : 插入排序法
- Selection Sort : 選擇排序法
- Bubble Sort
- e.g. : Nested Loops
int[] arr = {1,2,3,4,5};
for(int i = 0; i < arr.length; i++){
for(int j = 0; j < arr.length; j++){
System.out.println(arr[i]);
}
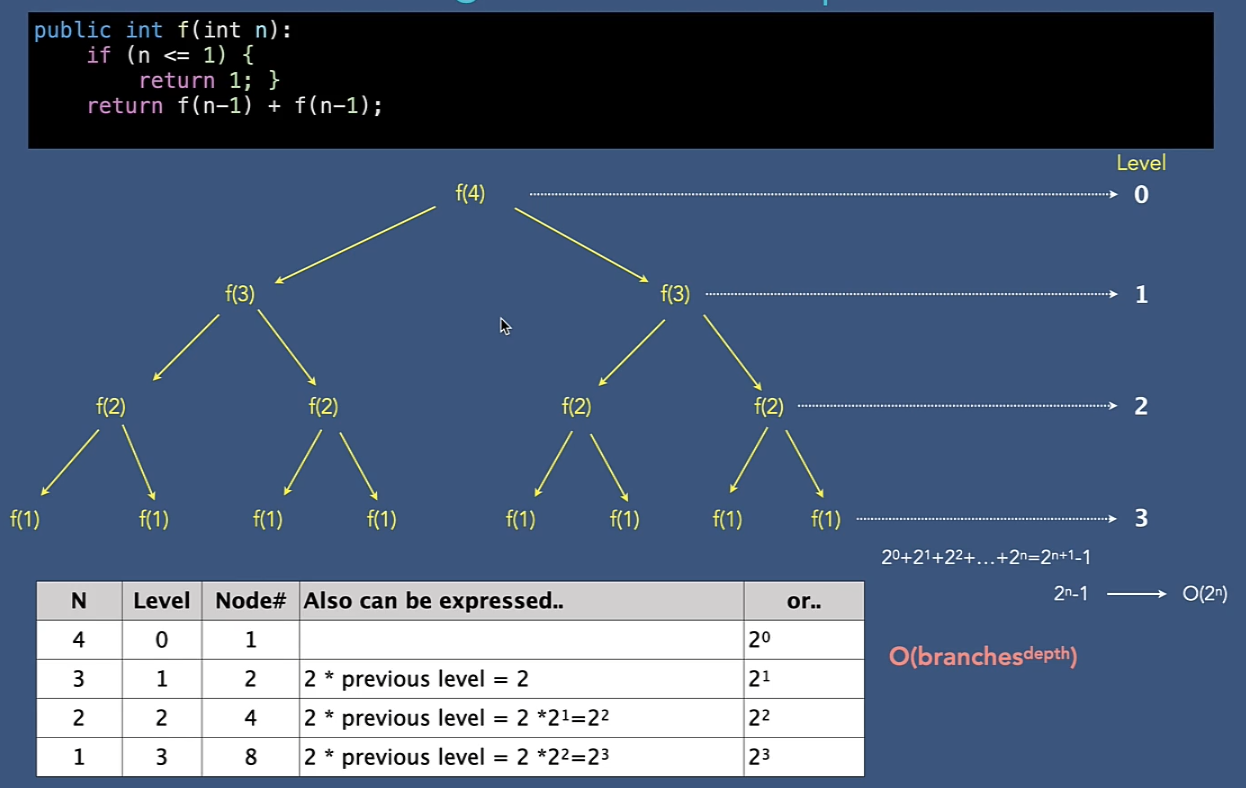
}O(2^n)
- Exponential
- 通常出現在使用 Recursive Algorithms 的情況
- e.g. : 費波那契數列
public int fibonacci(int n){
if(n == 0 || n == 1){
return n;
}
return fibonacci(n-1) + fibonacci(n-2);
}O(N!)
- Factorial Time
- Traveling Salesman Problem
- 將每個元素都加上迴圈
Space of Complexity
- 空間複雜度
- an array of size n
- Matrix = an array of size n * n
Examples
- 空間複雜度:
static int sum(int n){
if(n <= 0){
return 0;
}
return n + sum(n-1);
}- 空間複雜度:
static int pairSumSequence(int n){
var sum = 0
for(int i = 0; i <=0; i++){
sum = sum + pairSum(i, i+1);
}
return sum;
}
static int pairSum(int x, int y){
return x + y;
}去除常數 - 留下最主要影響的項目
Drop Constant
Drop Non Dominant Terms
Runtime 的增加, 相乘
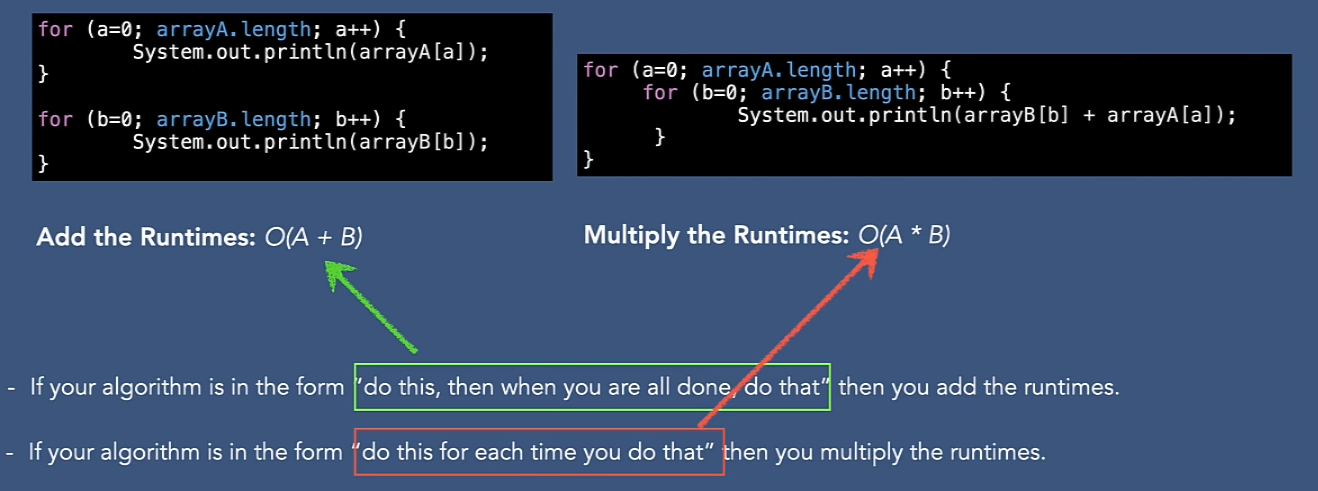
使用Big-O,衡量時間複雜度
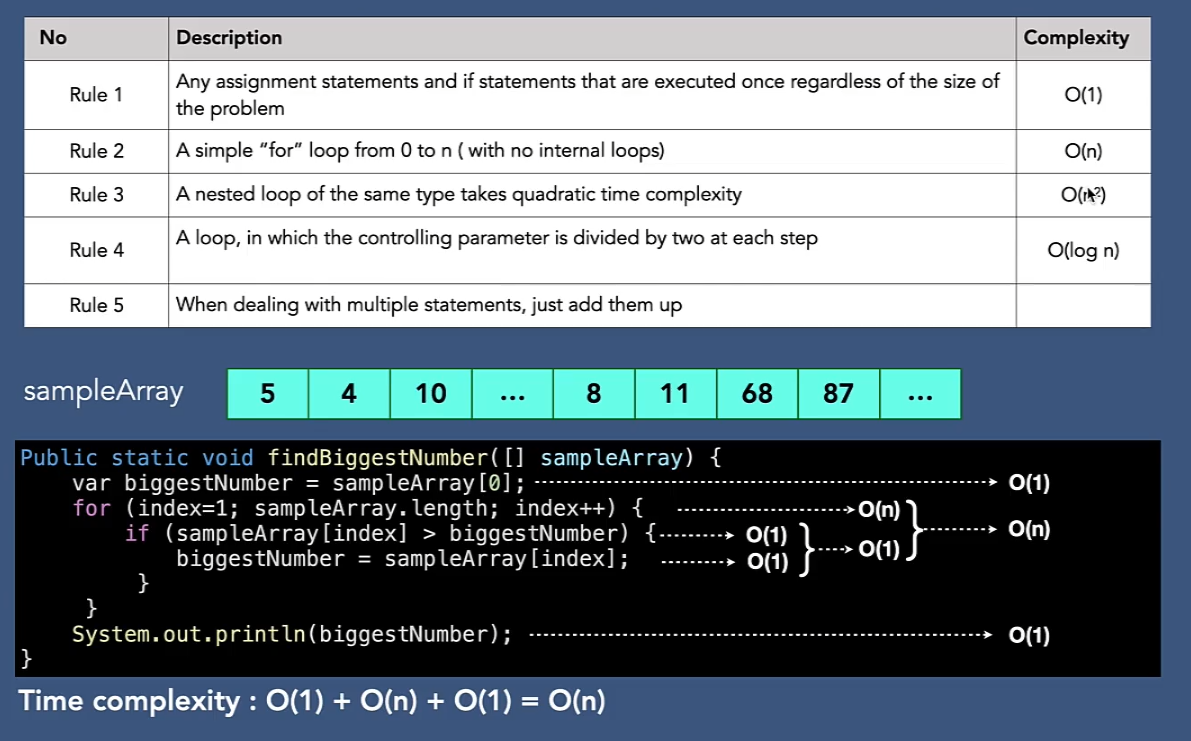
計算遞迴演算法時間複雜度-I
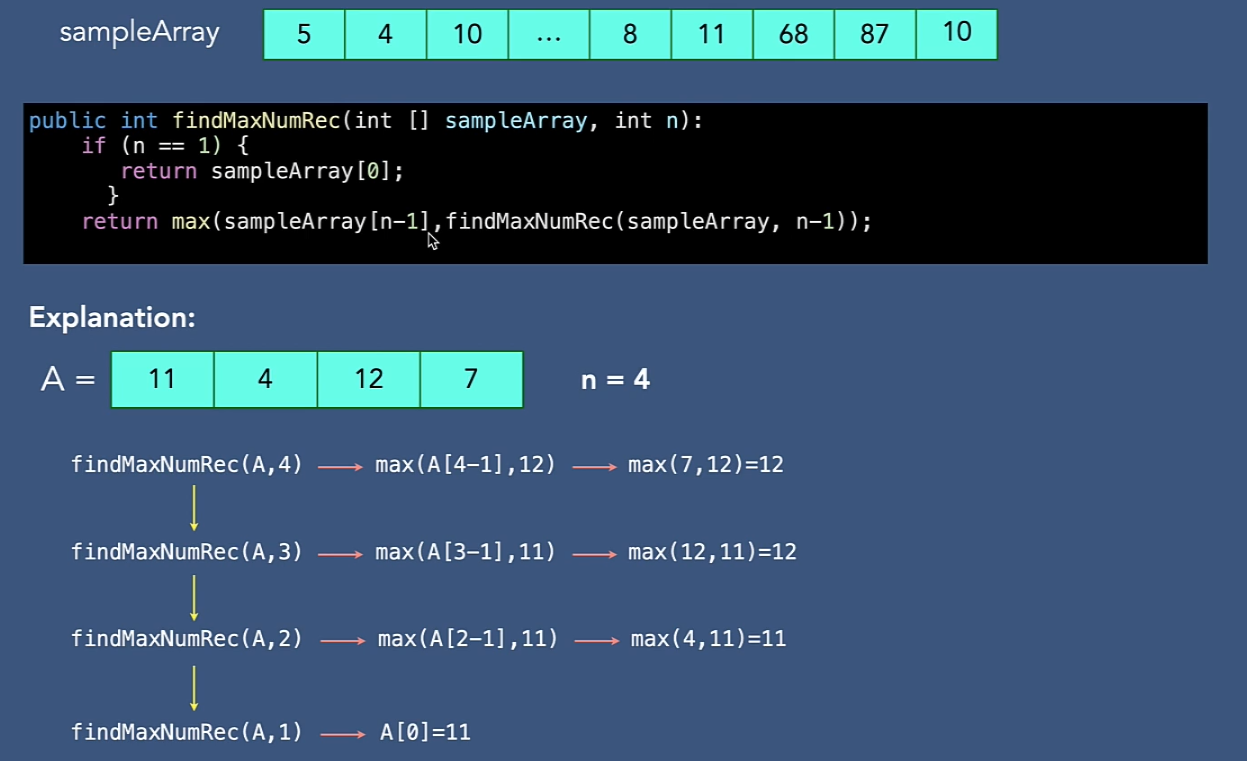
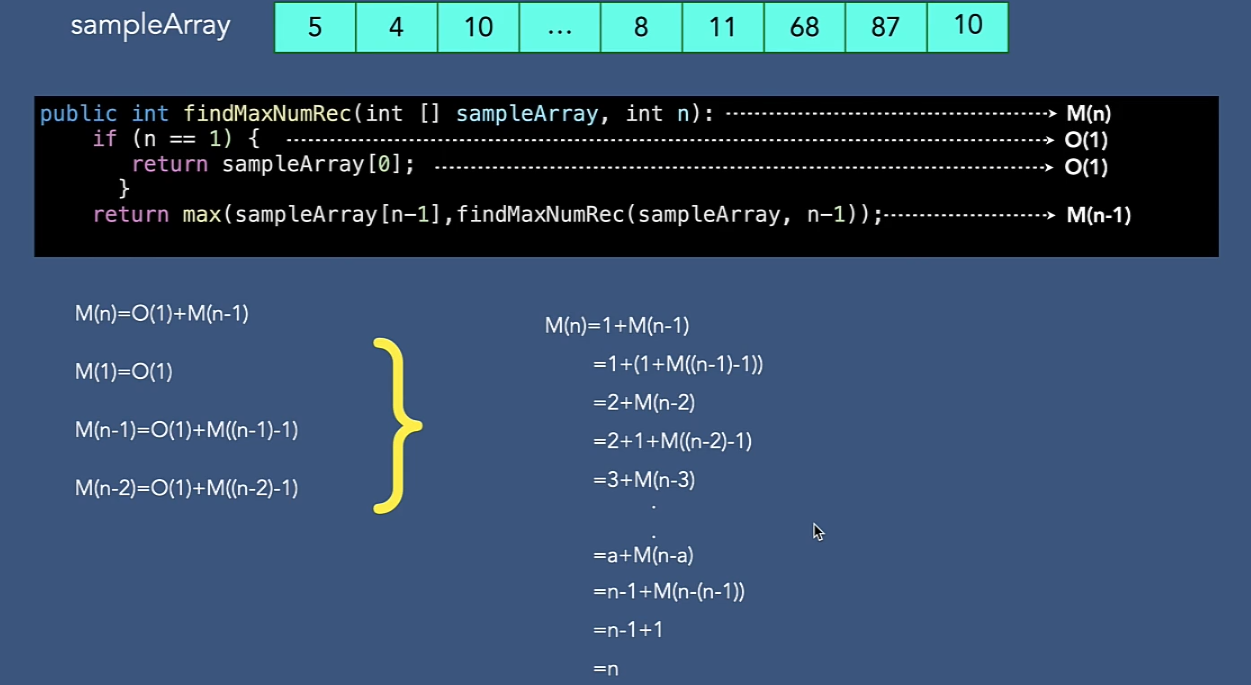
計算遞迴演算法時間複雜度-II