Asymptotic Analysis
漸近 解析 - アルゴリズムの時間 と空間 計算量 の分析
良いコードとは
- Readable(可読性 )
- Scalable(スケーラブル)の測定
は:
- 空間計算量 (Space Complexity):アルゴリズム実行 に必要 なメモリ空間
- 時間計算量 (Time Complexity):アルゴリズム実行 に必要 な時間
Big O は異 なるアルゴリズムの時間計算量 を測定 するために使用 され、 処理 するデータ量 が増加 するにつれて、プログラム実行時間 が増加 する割合
Asymptotic Notation
- 漸近 記法
- 分析結果
は最悪
ケース、最良
ケース、平均
ケースなどに分類
できる
- Big-O ( Ο ):アルゴリズム時間関数 の上限 (Upper bound)、つまり最悪 の場合 の実行回数
- Omega ( Ω ):アルゴリズム時間関数 の下限 (Lower bound)
- Theta ( θ ):アルゴリズム時間関数 の上限 と下限 の間
Time of Complexity
- 時間計算量
| Complexity | Name | Desc. |
|---|---|---|
O(1) | Constant | 配列 の特定要素 へのアクセス |
O(N) | Linear | 配列要素 のループ処理 |
O(log N) | Logarithmic | 配列要素 の検索 |
O(N²) | Quadratic | 配列 の各 インデックスを2回 参照 |
O(2^N) | Exponential | フィボナッチでの二重再帰 |
O(1)
- 定数
時間
- 配列 要素 へのランダムアクセス
- 連結 リストの先頭 への挿入
- 配列読 み取 り
- ループがなく、実行時間 は入力 データ量 の増加 に影響 されない
O(log n)
- 対数 時間
- Binary Search(二分探索
)
- ソート済 みの配列 で目標値 の位置 を見 つける探索 アルゴリズム
- 各 ステップで配列 の半分 が除外 される
O(n)
- 線形探索
: コレクションの要素
を1つずつ反復処理
- 配列要素 のループ処理
- 連結 リストの探索
O(n log n)
- 準線形
時間
- Quick Sort
- Merge Sort : マージソート
- Heap Sort
- 通常 、ソート操作 で使用 される
O(n²)
- 二乗
時間
- Insertion Sort : 挿入 ソート
- Selection Sort : 選択 ソート
- Bubble Sort
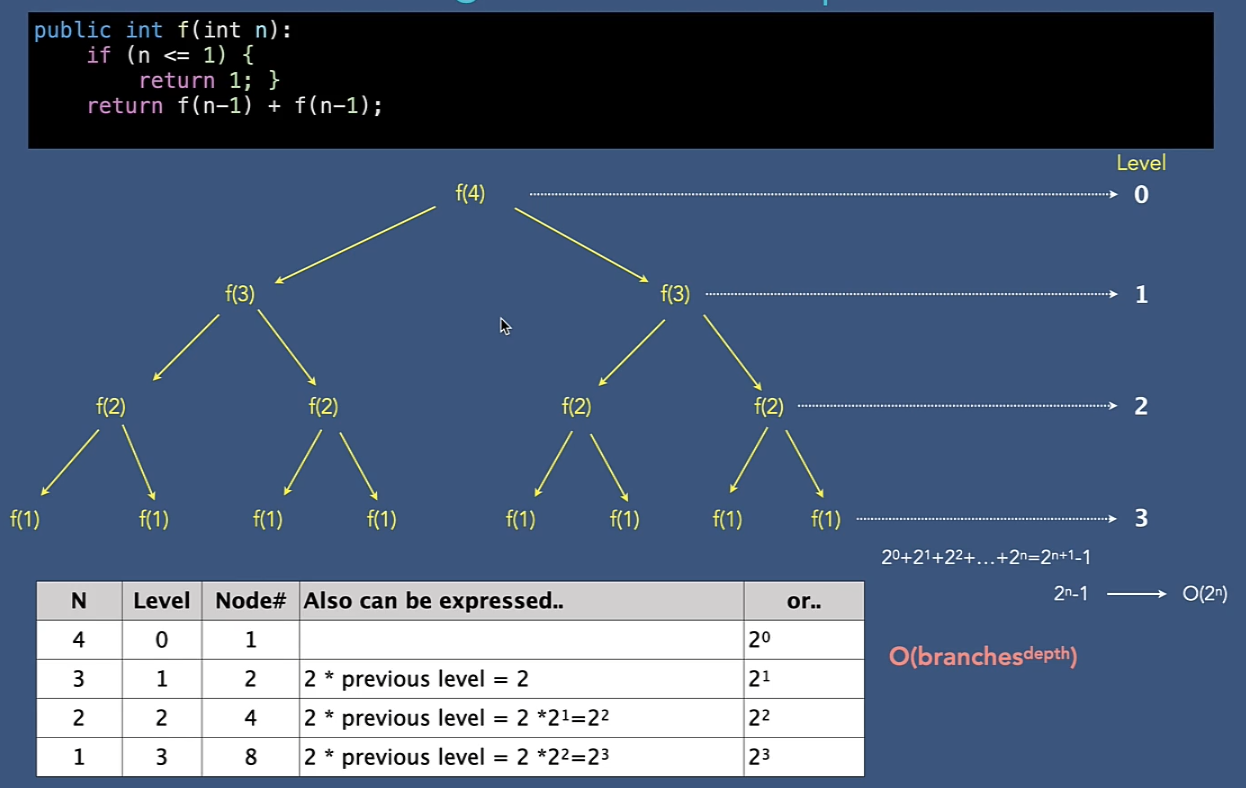
O(2^n)
- 指数 時間
- 通常 、再帰 アルゴリズムで発生
- 例 : フィボナッチ数列
O(N!)
- 階乗 時間
- 巡回 セールスマン問題
Space of Complexity
- 空間計算量
- サイズ n の配列
- 行列 = サイズ n * n の配列
定数を除去 - 最も影響を与える項目を残す
Drop Constant
Drop Non Dominant Terms
Runtime の増加、乗算
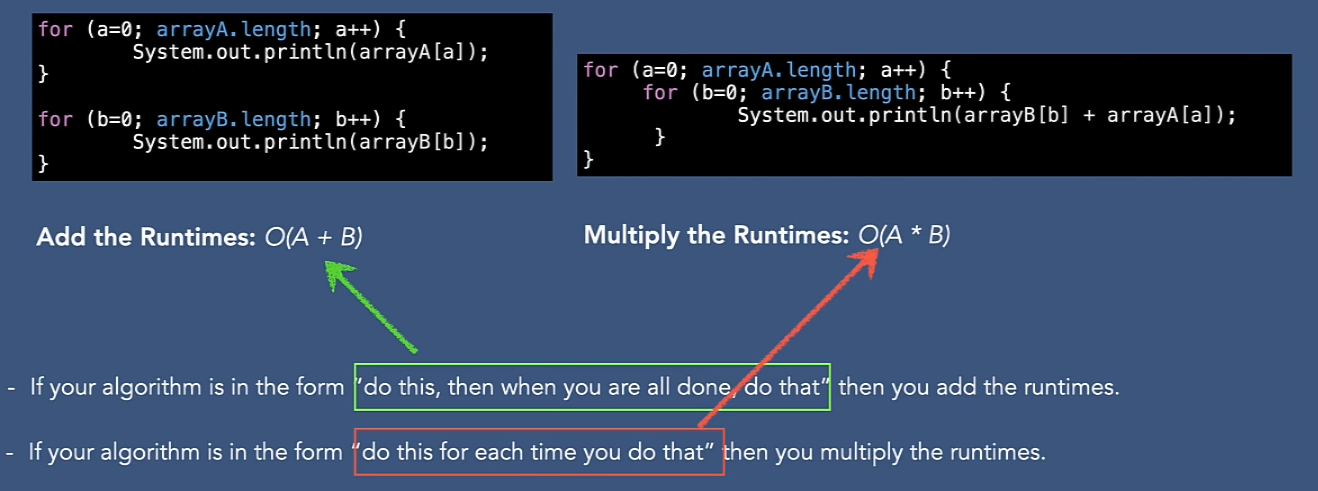
Big-Oを使用した時間計算量の測定
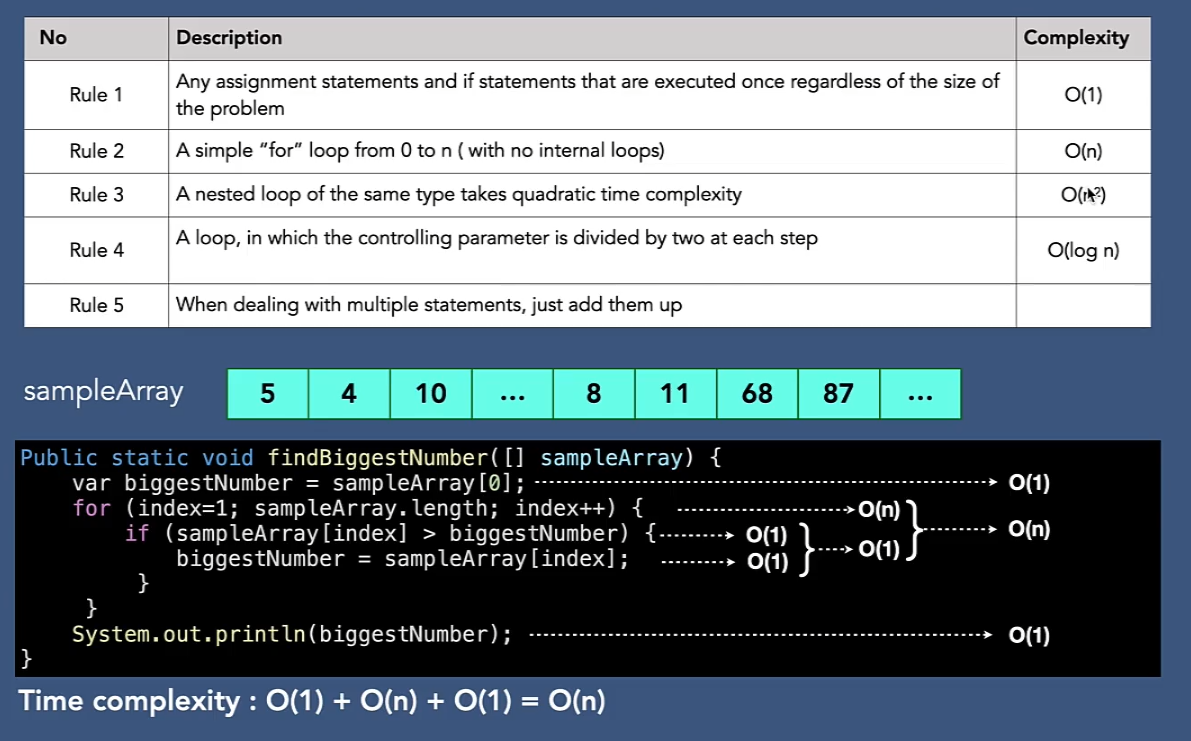
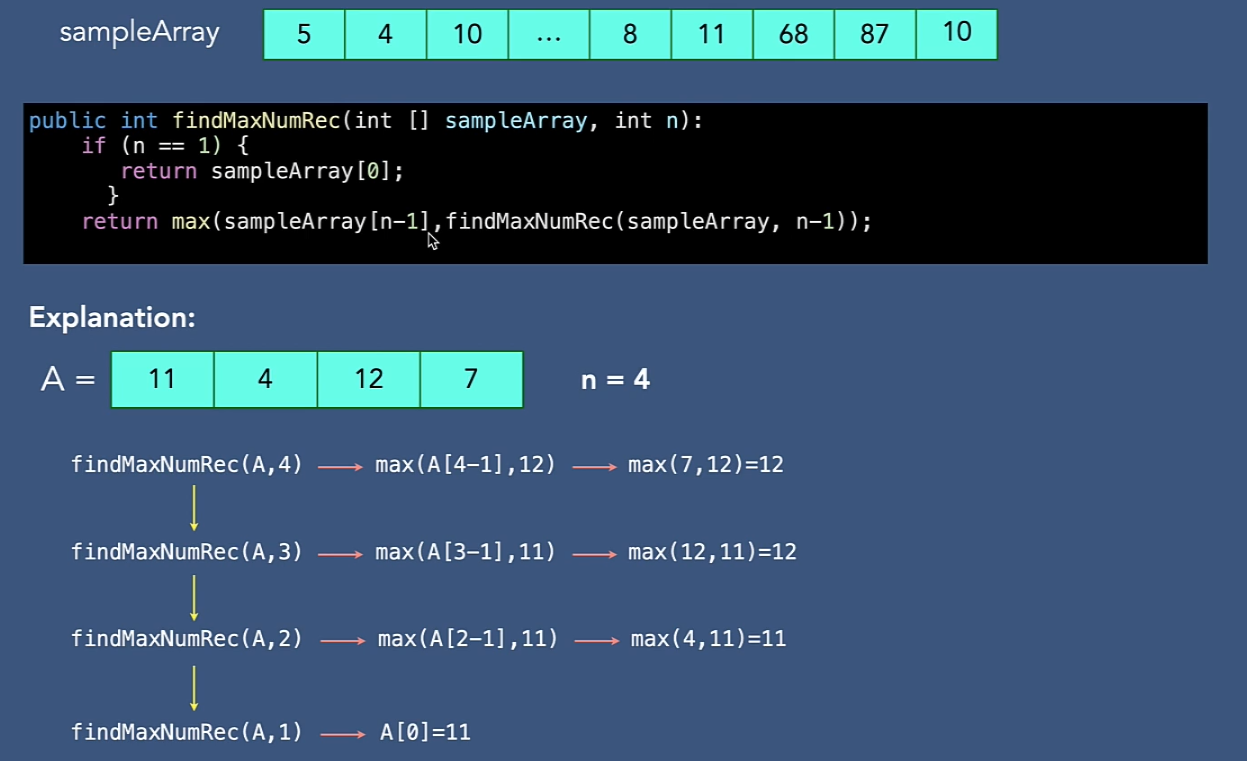
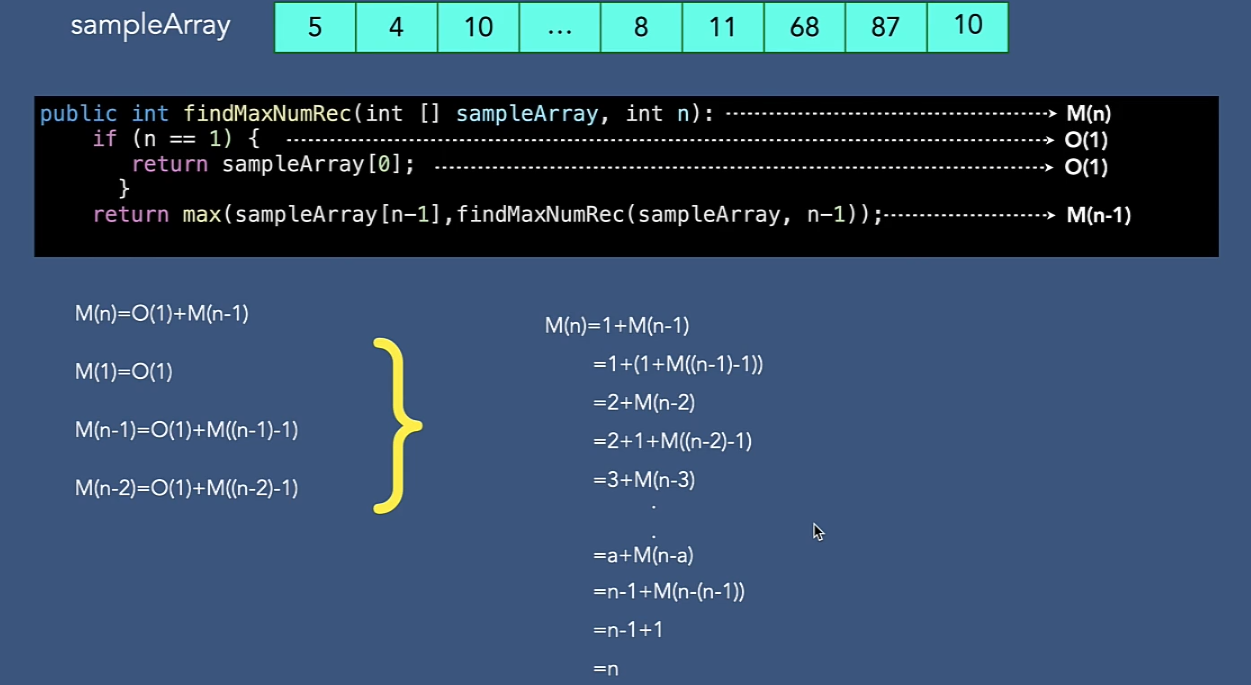
再帰アルゴリズムの時間計算量計算